Programmer Lifestyle

Sunday, February 16, 2014

How To Create Overlay Css

The usage of overlay css is to block the user interaction. It can be done by used 1 <div> element and Css styling.

Below is the source code to create overlay.

<!DOCTYPE html>
<html xmlns="http://www.w3.org/1999/xhtml">
<head>
    <title>Overlay</title>
    <style>
       #ImOverlay{
           position:absolute;
           width: 100%;
           height:100%;
           background-color:rgba(0,0,0,0.8);
           display:none;
       }
    </style>
</head>
<body>
    <div id="ImOverlay"></div>
    <p>How overlay works ?</p>
    <button id="btnOverlay" type="button" onclick="ShowOverlay();">Show Overlay</button>
</body>
</html>
<script type="text/javascript">
    function ShowOverlay() {
       document.getElementById("ImOverlay").style.display = "block";
    }
</script>

Tuesday, July 31, 2012

Factorial Computation Using Iteration ( Programming Language C )

This post will show the source code of factorial computation using iteration. In mathematics, the factorial of a non-negative integer n, denoted n!, is the product of all positive integers less than or equal to n. For example:

5! = 5 x 4 x 3 x 2 x 1 = 120

Iteration means the act of repeating a process usually with the aim of approaching a desired goal or target or result. In this case, for loop is represent the Iteration.

Source Code

Code::Blocks

#include <stdio.h>
#include <conio.h>

void main()
{
    int fact (int);
    int number,factnum;

    printf("\nEnter a positive number: ");
    scanf("%d", &number);
    factnum = fact(number);
    printf("\nFactorial number for %d\! = %d", number,factnum);

    getch();
}

int fact (int number)
{
    int i,fact=1;

    for (i=number;i>1;i--)
    {
        fact=fact*i;
    }

    return fact;
}

Wednesday, July 25, 2012

Facebook Social Plugins: Like Button

The Facebook Like Button lets users share pages from your site back to their Facebook Profile with one click. For example:

Facebook Like Button

The Like button lets a user share your content with friends on Facebook. When the user clicks the Like Button on your site, a story appears in the user's friends' News with a link back to your website. For example:


A story appear in the Facebook when user clicks the Like Button.

Follow the steps bellow to embed Like Button to your blog.

Step 1:


Go to Layout

Go to layout of the blog.

Step 2:

Add Gadget

Click "Add Gadget" and select "HTML/ JavaScript".

Step 3:

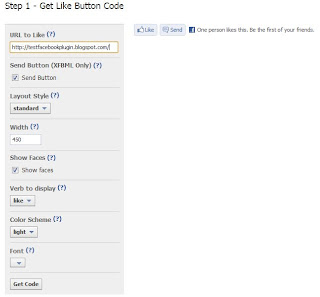Facebook page for the code generator of Like Button

Go to the following address http://developers.facebook.com/docs/reference/plugins/like/ and enter the URL of your blog (You also can leave it empty. But it might affect the SEO of your blog.). Then click the button "Get Code".

Step 4:

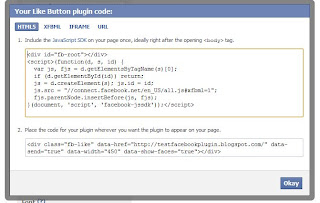Code generated by Facebook

After you click the "Get Code" button, Facebook will generated the code as show as above. First part is JavaScript SDK and second part is code used to the Like Button in your blog.

Step 5:

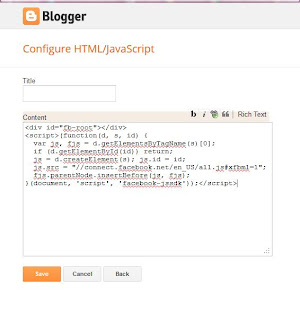Paste first part of code to Content

Leave the title empty. Copy the first part of the code and paste it in the "Content" and click "Save"

Step 6:

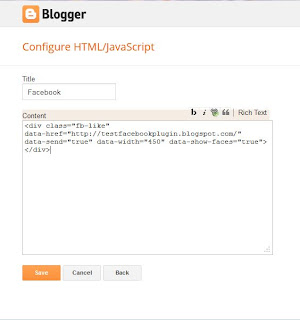Add second part of code

Click "Add Gadget" from layout again and select "HTML/ JavaScript". In the title textbox, enter "Facebook" and copy and paste second part of code to the "Content". Then click "Save"

Step 7:

Like Button

Go back to your blog. Facebook Like Button should appear in your blog....^^

Histogram Equalization

Histogram Equalization is a popular technique for enhancing image contrast. Histogram Equalization can change in image brightness that is become much brighter than input image. Histogram Equalization has been a simple effective image enhancement technique but Histogram Equalization tends to change the brightness of an image significant, causing unnatural contrast enhancement. Besides that, Histogram Equalization is not commonly used on scanning electron microscope (SEM) image this method causes significant change on the input image brightness and introduce undesirable artifacts. The mean brightness Histogram Equalization image is always the middle gray level regardless of the input image mean, thus this characteristic is not desirable in application where brightness preservation is needed. As a result, Histogram Equalization is not commonly used in consumer electron because it could cause annoying distortions like excessive brightness change, noise artifacts and brightness saturation.

Source Code

Matlab version R2011b (7.13.0.564)

%original Image
originalImage=imread('cameraman.tif');

%define the size of image after Histogram Equalization
HEImage=uint8(zeros(size(originalImage,1),size(originalImage,2)));

%calculate total pixels of original image
numofpixels=size(originalImage,1)*size(originalImage,2);

%obtain intensity by using imhist
[intensity grayLevels]=imhist(originalImage);

%calculate the pdf of original image
pdf=intensity/numofpixels;

%calculate the cdf of original image
cdf=cumsum(pdf);

%convert to Histogram Equalization image by replace the pixels of original image
for i=1:size(originalImage,1)
    for j=1:size(originalImage,2)
        HEImage(i,j)=round(cdf(originalImage(i,j)+1)*255);
    end
end

%showing and plotting the original image and image after Histogram Equalization
subplot (2,2,1);
imshow(originalImage);
title('Original Histogram');
subplot (2,2,2);
imhist(originalImage);
subplot (2,2,3);
imshow(HEImage);
title('Histogram equalization');
subplot (2,2,4);
imhist(HEImage);

Result:

Before and After Histogram Equalization